The draw is also psychologically psychologically?Come in and see how the probability of winning the

Lottery and game drawing cards, all kinds of lottery activities are full of our lives. For merchants who hold a lottery, fancy raffle can efficiently attract customers; for consumers participating in the lottery, smaller investment has a probability of gutting a generous return.

But when participating in the lottery, do you have doubts: "There are so many prizes, many people have won the prize, why have I never draw?"

Of course, the possibility of unable to draw a prize does not rule out the possibility of black -hearted merchants, but today we are going to explore the psychology and probability of the fair lottery.

PART.1

Why do you always feel that you can win the prize?

It is clear that the probability of winning most of the lottery in life is very low.

For a simple example, friends who often play mobile games may be very clear that the probability of getting rare characters is generally below 2%; and the common lottery game mechanism "two -color ball", the probability of winning the prize is only 6.71%(based on the blessing of the colorful balls of the blessing color, the color ball of the blessing color is the ball as the ball as the ball. For example, a single bet, including the first prize to the sixth prize).

As for the first prize of the "Super Award", the probability of winning the prize is only about 17 million -in -one. Of course, there are rules such as double -color balls and duplex betting. We only make simple examples here.

It can be seen that the winning people belong to the "small lucky one" in the crowd.

Since the probability of winning the prize is so low and the number of winners is so small, why do we feel that everyone around you is winning? This needs to be considered from a psychological perspective.

First of all, in order to attract more people to come to the lottery, the organizers will use the winning people to propagate, and the media of various media are also willing to report the lucky one of the awards. In the people, the participants who have not won the prize have been ignored, and we have the illusion of "everyone is winning."

This logical error is psychologically called the survivor deviation, that is, people only see the result of a certain screening and did not realize the process of screening. Therefore Essence

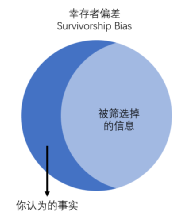
(Picture source: Author self -made)

After the screening of merchants and media, we only paid attention to the winners, but we did not pay attention to those who did not win the prize, thereby ignoring the fact that "the probability of winning the prize is very low".

Secondly, as the participants in the lottery, we subjectively want ourselves to win. Therefore, we usually put more attention on the winners and deliberately ignore the existence of the unsuccessful winner.

And this kind of thinking misunderstanding is called confirmation bias, also known as confirmation bias and verification bias), that is, when we judge our assumptions and make decisions, we usually feel that supportive arguments are more convincing At the same time, it will also find information consistent with yourself intentionally or unintentionally, and ignore the information that may be inconsistent with it.

(Picture source: Author self -made)

To put it simply, "we always tend to believe in what we want to believe."

In the raffle, we assume that we will win the prize, and then the brain will continue to screen the evidence (a few winners) that supports our assumptions, and selectively ignore the evidence of threatening our assumptions (most of the winners), As a matter of subjective ignoring the fact that "the probability of winning a prize is very low" at the subjective level.

PART.2

Is the lottery successful?

In the lottery such as drawing and touching prizes, because the number of prizes with a lot of prizes will be worried that when the lottery is drawn by the lottery, the person who will be drawn after the draw will not be able to draw it, so the person who will win the prize later will win the prize. The probability will be lower than those who are drawn first. But is this really the case?

(Picture source: Author self -made)

Let's first clarify the basic concepts in probability.

The first is a random test, that is, for a test, if the test can be repeated under certain conditions, there are more than one, and each time we test, we cannot definitely appear. Such a test is called random trial. In random trials, the most basic and unreasonable results are called basic results or basic events.

For the lottery, we cannot determine which ticket is the draw on each raffle, so this lottery is a random event, and each drawing ticket is a basic event.

In addition, the lottery is also a classical summary, that is, the number of basic events is limited and may be equal. For the classical type, we have the probability of an event A. The total number of basic events contained in A ÷ the total number of basic events contains.

Next is the condition probability, that is, the probability of event A under the condition of event B, indicating At the time of AB,

< /g> < /g>

Deformation can get . We still analyze this problem from an example.

Suppose a lottery has 10 vouchers, of which 1 vouchers. Then according to the classical type, there are 10 possible results in the first lottery, one of which is the winning prize, so the probability of the first draw drawing voucher is the "> Can't draw it as an event A, the second time is drawn as event B). In the second lottery, according to the results of the first lottery, there are two situations: two cases:

1. For the first time, I got a lottery ticket, and the remaining 9 of the prizes were not brought.

2. For the first time, the prize ticket was not drawn, and one of the 9 vouchers in the prize pool was brought. According to the classical summary, the probability of obviously drawing the lottery (recorded as an event C) at this time is .

It should be noted that the probability obtained in the second case is actually a conditional probability. That is, under the condition of not being drawn for the first time, the probability of the second time the ticket is drawn. Formula = "P (C | A) = RAC19"> , it is not the real probability of the second time you get the ticket. ROLE = "Presentation" Tabindex = "0" CTXTMENU_COUNTER = "76" Data-Formula = "P (B ) "> < g data-mml-node = "mi" /> .

If we want to draw the lottery ticket for the second lottery, the situation 2 will appear and get the ticket ticket, that is, the event A and event C occur at the same time, recorded as , the conditional probability formula we introduced earlier, can be obtained:

"> < /> g data-mml-node = "mi" transform = "translate (12091.6, 0)" /> < /> < /> g data-mml-node = "mo" transform = "translate (2955.8, 0)" />

"Currentcolor" file = "Currentcolor" stroke-width = "0" transform = "matrix (1 0 0-1 0)"> "> < / g> < /g> < /> Rect width = "1200" height = "60" x = "120" y = "220"/>

It can be concluded that the conclusion g data-mml-node = "mo" transform = "translate (1890, 0)" /> That is, the probability of the first lottery and the second lottery draw is the same. By analogy, the winning/unintentional prize before the lottery is generally classified as two events. Using this method, we can expand to the third and tenth draws. You will find that the probability of winning the prize is the same.

Therefore, in the order draw, the probability of winning the prize is the same.

PART.3

How to choose a Monte problem?

The problem of Monte is a very interesting issue related to the probability of the probability. It is also commonly known as the "sheep door problem". The content is as follows:

You participated in a TV show, there are three doors in front of you, one of which is a car behind one door, and the remaining two doors are one sheep.

The host closed these three doors and let you choose one of them. If the door you choose is a car, this car is yours, but if you choose the door behind you are sheep, you will not be able to get anything.

After you make your own choice, you know that the host of the car position opened one of the remaining two doors for you, and a sheep behind the door.

At this time, the host tells you that you have another chance to choose. So, will you adhere to your previous decision, or will you choose another door that has not been opened?

Obviously, in the initial choice, can you choose a car, which is in line with the classical summary we just mentioned. = "111" data-formula = "rac13"> < /g> .

After the host excluded a wrong answer for you, there are only two doors left-one sheep and one car. No matter which door is selected, the probability of obtaining a car seems to be ; but if you choose to change the door, the probability of getting a car will rise to < g data-mml-node = "mfrac">

This answer sounds intuitive, isn't it? After the host opens the door to eliminate a sheep, the probability of two doors should be 50%of the probability of getting the probability of obtaining a car?

Don't worry, let's analyze this problem from the perspective of probability theory.

As shown in the figure below, there are three basic results in the arrangement behind the door:

(Picture source: Author self -made)

From the figure we can see that no matter which door you choose, the probability of getting a car is one -third. After you choose a door (assumed to be the door 1), there are still three cases. At this time, the host opened a door with a sheep for you, and there were two doors left on the scene:

(Picture source: Author self -made)

There are still three possible situations: Case 1: The car is at Gate 1. The host excludes any of the 2 or 3 gates. You can get a car without changing it.

Situation 2: The car is at Gate 2. The host excludes the sheep behind Gate 3. If you can't change the car, you can get the car.

Situation 3: The car is at Gate 3. The host excludes the sheep behind Gate 2. If you can't change the car, you can get the car.

Because the probability of the three situations is still equal, this problem is still in line with the classical type. It is not difficult to conclude that the probability of choosing not to change the door is ; Choose the door to change the door, the probability of getting a car is Essence

In order to achieve marketing purposes, various businesses often carry out various types of lottery activities, and the rules of the lottery are also diverse. But in fact, these dazzling raffle rules are basically beneficial to merchants. You may make a small profit, but the merchants will never lose.

In the face of these complicated lottery, only if you understand the basic psychological theory and master the probability knowledge, will you not be induced by the black -hearted merchant, and will not be deceived by the complicated lottery rules.

In the end, it is important to emphasize that moderate participation in the lottery can be a pastime, but must not be used to make the lottery, and it should not be overly hoped that the lottery is "wealthy overnight", and "gambler psychology" is not advisable!

Produced: Popular Science China

Author: Dietang Science

Producer: China Science Popularization Expo

- END -